
The variance and the standard deviation are dispersion measures that quantify the grade of variability, spread or scatter of a variable. Along with measures of central tendency, statistical dispersion measures are used to describe the properties a distribution. In this tutorial you will learn how to calculate the variance and the standard deviation in R with the sd and var functions.
The variance, denoted by \(S^2_n\) , or \(\sigma^2_n\) is the arithmetic mean of the square deviations of the values of the variable respect to its mean. This is,
being \(n\) the number of observations and \(\bar\) the mean of the variable.
The denominator n-1 is used to give an unbiased estimator of the variance for i.i.d. observations.
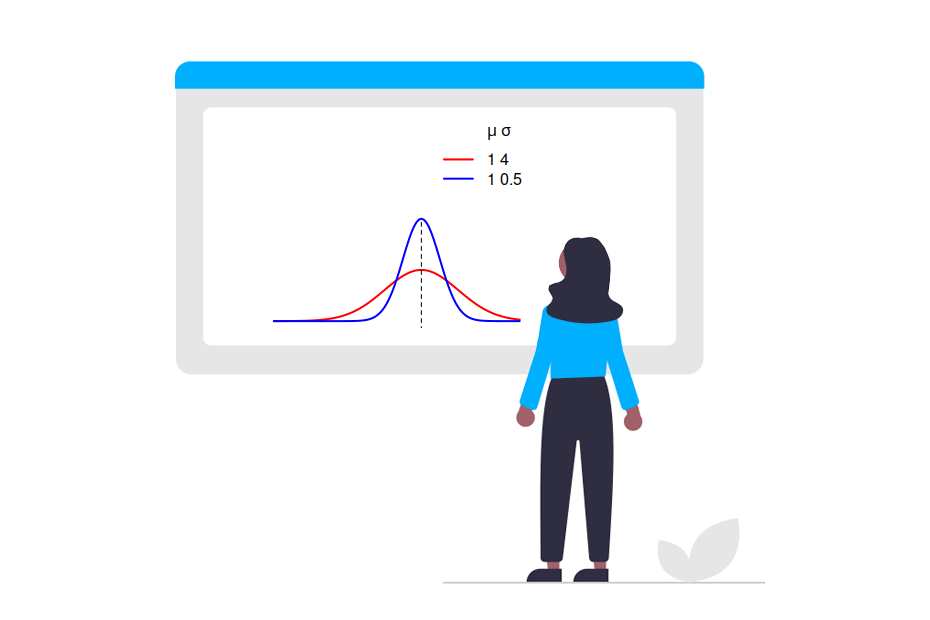
The variance is always positive and greater values will indicate higher dispersion.
When using R, we can make use of the var function to calculate the variance of a variable. Considering the following sample vector you can calculate its variance with the function:
# Sample vector x Note that the function provides an argument named na.rm that can be set to TRUE to remove missing values.
The standard deviation is the positive square root of the variance, this is, \(S_n = \sqrt\) . The standard deviation is more used in Statistics than the variance, as it is expressed in the same units as the variable, while the variance is expressed in square units.
In R, the standard deviation can be calculated making use of the sd function, as shown below:
# Sample vector x Similarly, we can calculate the variance as the square of the standard deviation:
# Sample vector x The sd function also provides the na.rm argument, that can be set to TRUE if the input vector contains any NA value. Otherwise, the output of the function will be an NA .